【Python数据分析案例（2025）】01—基于XGboots与支持向量机等多模型对比下的营销数据对用户购买行为的影响

网盘截屏

获取全部源码和数据，请点击购买，购买后无连接或其他异常，请联系我们QQ1919588043

1.项目介绍

在当今竞争激烈的市场环境中，了解客户行为和优化营销策略对企业的成功至关重要。为此，本项目的核心目标是通过对客户营销数据的分析，深入洞察影响客户购买行为的关键因素，从而提升营销活动的有效性。
1). 项目背景
本项目以某营销活动的数据集为基础，数据集包括客户的基本信息、购买行为、以及对多次营销活动的响应情况。企业希望通过这次数据分析，识别出哪些因素最显著地影响了客户对营销活动的响应以及最终的购买决策。
2). 数据介绍
数据集收集了在过去几年中收集的营销活动信息和客户购买记录。数据包括客户的个人属性（如出生年份、教育背景、婚姻状况）、家庭信息（如家庭收入、家中儿童和青少年数量）、购买行为（如各类产品的购买金额、不同渠道的购买次数）、以及客户对多次营销活动的响应数据。
3). 分析目标
识别关键影响因素：通过数据分析，识别显著影响客户响应营销活动的因素。帮助营销团队更好地理解客户特征与购买行为之间的关系。
优化营销策略：基于分析结果，为制定更加精准和高效的营销策略提供数据支持，以提高客户参与度和购买转化率。
预测客户响应：构建预测模型，预测未来营销活动中客户的响应概率，从而实现精准营销，优化资源配置。
4). 预期成果
通过本项目的分析，企业希望实现以下几个具体成果：
提高营销活动的响应率和投资回报率（ROI）。 增强客户关系管理，提升客户满意度和忠诚度。 建立数据驱动的决策机制，支持持续优化营销策略。 该项目的成功将为企业在市场竞争中获得更大的优势，同时为客户提供更加个性化和有价值的服务。通过数据的深度挖掘与分析，企业可以实现业务增长和客户体验的双赢。

2.数据说明

3.Python库导入及数据读取

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.sans-serif']='SimHei'  # 显示中文
plt.rcParams['axes.unicode_minus']=False # 显示负号

df=pd.read csv( marketing campaign.csv，sep='t).set index('ID)
df=df[lcol for col in df.columns if Unnamed' not in col]]
df. head (2)

4.数据预处理

4.1数据预览
查看数据基础信息

df.info()

可以看到大部分变量都是数值型，以及他们非空的数量
查看缺失值

df.isnull().sum()

# 观察缺失值
import missingno as msno
msno.matrix(df)

<AxesSubplot:>

Income存在24个缺失值，其他没有缺失值情况
非数值变量描述性统计

df.select dtypes(exclude=['int64',,float64’]).describe()

数值变量描述性统计

df.select dtypes(include=['int64','float64']).describe()

4.2一致性检验
从上面的分析可以看到数据基本都是数值型，但是存在一些类别型的变量需要做处理
缺失值处理

mean_income= df['Income']. mean()
#使用均值填充，Income’列中的缺失值
df['Income'].fillna(mean_income, inplace=True)
### 年龄计算
df['age'=2015-df[ Year Birth']

取值唯一的处理

# 取值唯一的变量删除
for col in df.columns:
	if len(df[col].value_counts()==1 :
		print(col)
		df.drop(col, axis=1,inplace=True)

Z_CostContact
Z_Revenue

做机器学习当然需要特征越分散越好，因为这样就可以在X上更加有区分度，从而更好的分类。所以那些数据分布很集中的变量可以扔掉。我们用异众比例来衡量数据的分散程度

#计算异众比例
variation_ratio_s=0.05
for col in df.select dtypes(exclude=['object’]). columns :
	df count=dflcol.value counts
	kind=df count.index[0]
	variation ratio=1-(df_count. iloc[0]/len(df[co1]))
	if variation ratio<variation ratio s:
		print(f’{co1}最多的取值为{kind}，异众比例为{round(variation_ratio,4)},太小了，没区分度删掉')
		df.drop(col,axis=1,inplace=True)

AcceptedCmp2 最多的取值为0，异众比例为0.0134,太小了，没区分度删掉
Complain 最多的取值为0，异众比例为0.0094,太小了，没区分度删掉

特征工程

df1=df.copy()  ##备份画图

## 日期字符串转为时间
df['Dt_Customer'] = pd.to_datetime(df['Dt_Customer'], format='%d-%m-%Y')
#计算客户注册时间的长短，转为数值型特征
df['Dt_Customer'] = (df['Dt_Customer'].max()-df['Dt_Customer']).dt.days

###	教育和婚育状态转为 数值型变量 #Education Marital_Status

# 对 'Education_encoded' 列进行标签编码
df['Education'], education_mapping = pd.factorize(df['Education'])
# 对 'Marital_Status' 列进行标签编码
df['Marital_Status'], marital_status_mapping = pd.factorize(df['Marital_Status'])

##查看映射规则
print("Education mapping:")
for i, category in enumerate(education_mapping):
    print(f"{category}: {i}")

print("\nMarital_Status mapping:")
for i, category in enumerate(marital_status_mapping):
    print(f"{category}: {i}")

df.info()

可以看到所有的变量都转为了数值型变量，可以进行如下分析

5.客户购买影响因素分析

5.1可视化分析

数值型变量画图

df1.select_dtypes(exclude=['object']).columns#.tolist()

#查看特征变量的箱线图分布
num_columns = ['Year_Birth', 'age','Income','Kidhome','Teenhome','Dt_Customer','Recency','MntWines', 'MntFruits', 'MntMeatProducts', 'MntFishProducts',
 'MntSweetProducts','MntGoldProds','NumDealsPurchases','NumWebPurchases','NumCatalogPurchases','NumStorePurchases','NumWebVisitsMonth',]# 列表头
dis_cols = 4                   #一行几个
dis_rows = len(num_columns)
plt.figure(figsize=(3 * dis_cols, 2.5 * dis_rows),dpi=128)
 
for i in range(len(num_columns)):
    plt.subplot(dis_rows,dis_cols,i+1)
    sns.boxplot(data=df[num_columns[i]], orient="v",width=0.5)
    plt.xlabel(num_columns[i],fontsize = 16)
plt.tight_layout()
#plt.savefig('特征变量箱线图',formate='png',dpi=500)
plt.show()

#画密度图，训练集和测试集对比
dis_cols = 4                   #一行几个
dis_rows = len(num_columns)
plt.figure(figsize=(3 * dis_cols, 2 * dis_rows),dpi=256)
 
for i in range(len(num_columns)):
    ax = plt.subplot(dis_rows, dis_cols, i+1)
    ax = sns.kdeplot(df[num_columns[i]], color="skyblue" ,fill=True)
    ax.set_xlabel(num_columns[i],fontsize = 14)
plt.tight_layout()
#plt.savefig('训练测试特征变量核密度图',formate='png',dpi=500)
plt.show()

分布都还好，从箱线图可以看到，部分变量有一些异常值，可以进行处理

分类型变量画图

df1.select_dtypes(exclude=['int64','float64']).columns

Index(['Education', 'Marital_Status', 'Dt_Customer'], dtype='object')

# Select non-numeric columns
non_numeric_columns =['Education', 'Marital_Status', 
                      'AcceptedCmp3', 'AcceptedCmp4', 'AcceptedCmp5','AcceptedCmp1', 'Response',]
# Set up the matplotlib figure with 2x4 subplots
f, axes = plt.subplots(3, 3, figsize=(9,9),dpi=128)
# Flatten axes for easy iterating
axes_flat = axes.flatten()
# Loop through the non-numeric columns and create a countplot for each
for i, column in enumerate(non_numeric_columns):
    if i < len(non_numeric_columns):  # Check to avoid IndexError if there are more than 8 non-numeric columns
        sns.countplot(x=column, data=df1, ax=axes_flat[i])
        axes_flat[i].set_title(f'Count of {column}')
        for label in axes_flat[i].get_xticklabels():
            label.set_rotation(45)

# Hide any unused subplots
for j in range(i + 1, 3*3):
    f.delaxes(axes_flat[j])
plt.tight_layout()
plt.show()

异常值处理

df_number=df.select_dtypes(include=['int64', 'float64'])

#X异常值处理，先标准化
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
df_number_s = scaler.fit_transform(df_number)

plt.figure(figsize=(20,8))
plt.boxplot(x=df_number_s,labels=df_number.columns)
#plt.hlines([-10,10],0,len(columns))
plt.show()

可以看到，很多变量都存在一些异常值，我们需要进行异常值处理

#异常值多的列进行处理
def deal_outline(data,col,n):   #数据，要处理的列名，几倍的方差
    for c in col:
        mean=data[c].mean()
        std=data[c].std()
        data=data[(data[c]>mean-n*std)&(data[c]<mean+n*std)]
        #print(data.shape)
    return data

df_number=deal_outline(df_number,df_number.columns,5)  #5倍的方差之外都删除
df_number.shape

### 处理完成后将数据筛选给原始数据
df=df.loc[df_number.index,:]
df.shape

可以看到数据量从2240变成了2212，异常值的被过滤掉了

5.2相关性分析

corr = plt.subplots(figsize = (18,16),dpi=128)
corr= sns.heatmap(df.corr(),annot=True,square=True) #

##皮尔逊相关系数
correlation_matrix = df.corr()
response_correlation = correlation_matrix['Response'].drop('Response').sort_values(key=abs, ascending=False)
pd.DataFrame(response_correlation)

## 换斯皮尔曼相关系数
correlation_matrix = df.corr(method='spearman')
response_correlation = correlation_matrix['Response'].drop('Response').sort_values(key=abs, ascending=False)
pd.DataFrame(response_correlation)

根据给定的斯皮尔曼相关系数结果，我们可以分析哪些变量与目标变量 Response 具有较强的相关性。斯皮尔曼相关系数是一种衡量两个变量之间单调关系的统计量，适用于非线性且不需要假设正态分布的数据。以下是对这些相关性结果的分析：

• 强相关变量 AcceptedCmp5（0.328）：与 Response 呈现中等正相关，表明参与最近的营销活动可能显著提升响应率。
• AcceptedCmp1（0.293）：与 Response 有中等正相关，早期营销活动的接受情况也对响应有较好的推动作用。
• AcceptedCmp3（0.255）：表现出中等正相关，说明此活动的接受度对响应有一定的影响。
• NumCatalogPurchases（0.235）：目录购物次数与响应正相关，暗示通过目录购物的顾客更可能对促销活动做出响应。
• MntMeatProducts（0.223）和 MntWines（0.199）：肉类和葡萄酒的消费金额与响应之间存在一定的正相关性，表明高消费群体可能更易响应促销。
• 中等相关变量 Recency（-0.198）：与响应呈负相关，最近的消费时间越长，响应的可能性越小，这可能是由于顾客对品牌失去兴趣或忘记。
• Dt_Customer（0.195）：与响应正相关，可能表明注册时间更早的顾客更忠诚或对促销更感兴趣。
• MntGoldProds（0.183）：黄金产品消费与响应的正相关性暗示此类高端产品的购买者可能是重要的营销目标。
• 弱相关变量 NumWebPurchases（0.173）和 Income（0.160）：虽然有一些相关性，但都较弱，表明在线购买次数和收入对响应有一定影响，但不是主要因素。
• Teenhome（-0.159）：有青少年孩子的家庭响应率略低，可能是因为家庭责任或支出优先级的不同。
• MntFruits（0.149） 和 MntSweetProducts（0.137）：这些变量与响应率的正相关性较弱，影响不如前述变量明显。

与响应几乎无关的变量 Kidhome、NumStorePurchases、NumDealsPurchases、Year_Birth、age、Marital_Status、NumWebVisitsMonth、Education：这些与响应变量相关性很弱，可能在这个模型中作用有限。 总结 这些分析表明，过去营销活动的参与情况、购买行为（尤其是高消费产品）和客户的忠诚度（如注册时间）都是影响响应的重要因素。相对而言，家庭结构（如孩子数量）、线下购买行为以及教育程度对响应的影响较小。根据这些分析结果，营销策略可以更关注于高价值客户群体和历史营销活动的参与者，可能会获得更高的响应率。

5.3ANOVA

non_numeric_columns

exampledata=df1[non_numeric_columns]
exampledata.info()

学历对营销活动购买的影响

# 拟合单因子方差分析模型并输出方差分析表
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
#example8_2=pd.read_csv("example8_2.csv",encoding="gbk") 
model = ols(formula='Response~Education',data=exampledata[['Education','Response']]).fit()  #拟合方差分析模型
anova_lm(model,typ=1)

print(model.summary())

和相关性系数观察到的结果一直，学历对营销活动的购买行为没有太大的显著性差异，整体来看，教育水平对 Response 的解释能力相对较弱。 只有“博士”教育水平对 Response 具有统计显著性，也就是说拥有博士学位与更高的响应率之间存在显著关联。 由于模型的 R-squared 较低，可能需要进一步探索其他可能的影响因子，以提高模型的解释力。 可能需要检查数据的正态性假设或采用其他稳健或非参数的方法来验证结果。

接受广告活动对营销购买行为的影响

model = ols(formula='Response~AcceptedCmp3',data=exampledata[['AcceptedCmp3','Response']]).fit()  #拟合方差分析模型
anova_lm(model,typ=1)

print(model.summary())

AcceptedCmp3 的重要性: 从F值和p值的结果显示 AcceptedCmp3 对 Response 的影响显著，客户在这次活动中的参与与响应率有明显关联。

模型的解释力: 尽管 R-squared 较低，模型仍然展示了对 Response 的一定解释能力，特别是突出 AcceptedCmp3 的作用。

模型改进建议

考虑增加其他潜在影响因素来提高模型的解释能力。
检查数据和模型假设，尤其是对残差正态性假设的验证，可以使用更稳健或非参数的方法进行验证和建模。
实际应用意义: 在实际营销策略中，这意味着企业可以将资源更多地集中于那些在AcceptedCmp3营销活动中积极参与的客户群体，可能会获得更高的响应率和转化率。

通过这种分析，营销团队可以更好地理解哪些活动更能驱动客户响应，并据此优化未来的营销策略。

6.机器学习模型构建

6.1数据预处理

数据标准化

#取出X和y
X=df.drop(columns=['Response'])
y=df['Response']

# 进行标准化
#数据标准化
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X)
X_s = scaler.transform(X)
print('标准化后数据形状：')
print(X_s.shape,y.shape)

训练集测试集划分

#划分训练集和测试集
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X_s,y,stratify=y,test_size=0.2,random_state=0)
print(X_train.shape,X_test.shape,y_train.shape,y_test.shape)

### 查看训练和测试集的y的购买和不够买类别占比
y_train.value_counts(normalize=True)

两者比例类似，分布类似，可以进行训练

分类问题的评价指标体系

TP（True Positive）：真正类，被正确预测为正类的数量。 TN（True Negative）：真负类，被正确预测为负类的数量。 FP（False Positive）：假正类，被错误预测为正类的负类数量。 FN（False Negative）：假负类，被错误预测为负类的正类数量。

• 准确率（Accuracy）

准确率表示模型预测正确的样本数占总样本数的比例。

$$\text{Accuracy} = \frac{\text{TP} + \text{TN}}{\text{TP} + \text{TN} + \text{FP} + \text{FN}}$$

• 精准度（Precision）

精准度是指被预测为正类的样本中实际为正类的比例。

Precision=TPTP+FP

• 召回率（Recall）

召回率是指实际为正类的样本中被正确预测为正类的比例。

Recall=TPTP+FN

• F1 值（F1 Score）

F1 值是精准度和召回率的调和平均，用于综合考虑精准度和召回率。

$$\text{F1 Score} = 2 \times \frac{\text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}}$$

计算评价指标函数定义

from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
from sklearn.metrics import cohen_kappa_score
 
def evaluation(y_test, y_predict):
    accuracy=classification_report(y_test, y_predict,output_dict=True)['accuracy']
    s=classification_report(y_test, y_predict,output_dict=True)['weighted avg']
    precision=s['precision']
    recall=s['recall']
    f1_score=s['f1-score']
    #kappa=cohen_kappa_score(y_test, y_predict)
    return accuracy,precision,recall,f1_score #, kappa

6.2建立分类模型

使用十种机器学习模型进行对比

#导包
from sklearn.linear_model import LogisticRegression
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import GradientBoostingClassifier
from xgboost.sklearn import XGBClassifier
from lightgbm import LGBMClassifier
from sklearn.svm import SVC
from sklearn.neural_network import MLPClassifier

实例化分类器

#逻辑回归
model1 =  LogisticRegression(C=1e10,max_iter=10000)
 
#线性判别分析
model2 = LinearDiscriminantAnalysis()
 
#K近邻
model3 = KNeighborsClassifier(n_neighbors=10)
 
#决策树
model4 = DecisionTreeClassifier(random_state=7,max_features='sqrt',class_weight='balanced')
 
#随机森林
model5= RandomForestClassifier(n_estimators=1000,  max_features='sqrt',random_state=10)
 
#梯度提升
model6 = GradientBoostingClassifier(random_state=123)

#极端梯度提升
model7 =  XGBClassifier(objective='binary:logistic',random_state=1)

#轻量梯度提升
model8 = LGBMClassifier(objective='binary',random_state=1,verbose=-1)

#支持向量机
model9 = SVC(kernel="rbf", random_state=77)
 
#神经网络
model10 = MLPClassifier(hidden_layer_sizes=(16,8), random_state=77, max_iter=10000)
 
model_list=[model1,model2,model3,model4,model5,model6,model7,model8,model9,model10]
model_name=['逻辑回归','线性判别','K近邻','决策树','随机森林','梯度提升','极端梯度提升','轻量梯度提升','支持向量机','神经网络']

6.3模型的训练和评估

#遍历所有的模型，训练，预测，评估
df_eval=pd.DataFrame(columns=['Accuracy','Precision','Recall','F1_score'])
for i in range(10):
    model_C=model_list[i]
    name=model_name[i]
    model_C.fit(X_train, y_train)
    pred=model_C.predict(X_test)
    #s=classification_report(y_test, pred)
    s=evaluation(y_test,pred)
    df_eval.loc[name,:]=list(s)
    print(f'{name}模型完成')

逻辑回归模型完成
线性判别模型完成
K近邻模型完成
决策树模型完成
随机森林模型完成
梯度提升模型完成
[13:49:08] WARNING: C:/Users/Administrator/workspace/xgboost-win64_release_1.5.1/src/learner.cc:1115: Starting in XGBoost 1.3.0, the default evaluation metric used with the objective 'binary:logistic' was changed from 'error' to 'logloss'. Explicitly set eval_metric if you'd like to restore the old behavior.

D:\Anaconda\lib\site-packages\xgboost\sklearn.py:1224: UserWarning: The use of label encoder in XGBClassifier is deprecated and will be removed in a future release. To remove this warning, do the following: 1) Pass option use_label_encoder=False when constructing XGBClassifier object; and 2) Encode your labels (y) as integers starting with 0, i.e. 0, 1, 2, ..., [num_class - 1].
  warnings.warn(label_encoder_deprecation_msg, UserWarning)

极端梯度提升模型完成
轻量梯度提升模型完成
支持向量机模型完成
神经网络模型完成

df_eval.astype('float').style.bar(color='gold')

评价指标可视化

import matplotlib.pyplot as plt 
plt.rcParams['font.sans-serif'] = ['KaiTi']  #中文
plt.rcParams['axes.unicode_minus'] = False   #负号
 
bar_width = 0.4
colors=['c', 'b', 'g', 'tomato', 'm', 'y', 'lime', 'k','orange','pink','grey','tan']
fig, ax = plt.subplots(2,2,figsize=(10,8),dpi=128)
for i,col in enumerate(df_eval.columns):
    n=int(str('22')+str(i+1))
    plt.subplot(n)
    df_col=df_eval[col]
    m =np.arange(len(df_col))
    plt.bar(x=m,height=df_col.to_numpy(),width=bar_width,color=colors)
    
    #plt.xlabel('Methods',fontsize=12)
    names=df_col.index
    plt.xticks(range(len(df_col)),names,fontsize=10)
    plt.xticks(rotation=40)
    plt.ylabel(col,fontsize=14)
    
plt.tight_layout()
#plt.savefig('柱状图.jpg',dpi=512)
plt.show()

在本次模型评估中，我们对比了多种机器学习算法，以识别出最适合预测客户购买行为的模型。各个模型的性能通过四个主要指标进行衡量：准确率（Accuracy）、精确率（Precision）、召回率（Recall）和F1评分（F1 Score）。这些指标全面评估了模型的预测能力和稳定性。

从结果来看，梯度提升模型（Gradient Boosting）在各项指标上表现最为突出，准确率达到了0.878104，精确率为0.863146，召回率与F1评分分别为0.878104和0.862861。这表明梯度提升模型不仅在整体预测能力上优于其他模型，而且在平衡精确率与召回率方面也具有优势，能够有效捕捉客户的购买行为。

极端梯度提升（XGBoost）和神经网络模型在性能上也紧随其后，分别展现了较高的准确率和F1评分。XGBoost的F1评分为0.864826，略高于梯度提升，显示了其在处理复杂数据集时的强大能力。神经网络同样展现了出色的性能，特别是在精确率和F1评分上，反映了其在捕捉非线性关系方面的潜力。

其他模型如随机森林（Random Forest）和支持向量机（SVM）虽然准确率达到了0.864560，但在精确率和F1评分上略显逊色。这可能是由于这些模型在处理高维度数据或捕捉复杂模式时的局限性。

相比之下，逻辑回归和线性判别分析等线性模型表现相对一般。这些模型的准确率和F1评分略低，可能由于它们对线性关系的假设限制了其在复杂数据集上的表现。然而，逻辑回归模型的精确率达到0.840189，仍然体现了其在某些场景下的有效性。

综合考虑各模型的表现，梯度提升模型因其优异的整体性能而成为最终选择。其出色的预测能力和指标平衡性使其成为在营销场景下预测客户行为的理想候选。后续工作将专注于模型的进一步优化及其在实际应用中的部署，以推动更精准的市场策略和客户管理。

6.4模型的选择和超参数优化

营销场景下，我们比较关注准确率，梯度提升的准确率是最高的，因此我们选择梯度提升作为最终的模型来进行超参数搜索优化

from sklearn.model_selection import KFold, train_test_split, GridSearchCV, PredefinedSplit
rf_model =  GradientBoostingClassifier(random_state=123)
test_fold = np.concatenate((
    -1 * np.ones(len(X_train), dtype=int), 
    np.zeros(len(X_test), dtype=int)
))

# 创建预定义分割
ps = PredefinedSplit(test_fold)

# 定义要搜索的超参数
param_dict = {
    'n_estimators': [100, 500, 700],
    'learning_rate': [0.01, 0.1, 0.2],
    'max_depth': [3, 5, 7]
}

# 使用GridSearchCV进行超参数调优
clf = GridSearchCV(
    GradientBoostingClassifier(random_state=123), 
    param_dict, 
    cv=ps, 
    verbose=1
)

# 进行拟合
clf.fit(X_s, y)

# 输出最佳得分和最佳参数
print("Best Test Set Accuracy:", clf.best_score_)
print("Best Parameters:", clf.best_params_)

Fitting 1 folds for each of 27 candidates, totalling 27 fits
Best Test Set Accuracy: 0.8961625282167043
Best Parameters: {'learning_rate': 0.01, 'max_depth': 3, 'n_estimators': 700}

将搜索出来的这个超参数代入模型去训练

model=GradientBoostingClassifier(learning_rate= 0.01,max_depth=3, n_estimators=700,random_state=123)
model.fit(X_train, y_train)
y_pred=model.predict(X_test)
evaluation(y_test,y_pred)

(0.8803611738148984, 0.8665986650958682, 0.8803611738148984, 0.861873226139047)

效果没有太多提升，基本平准

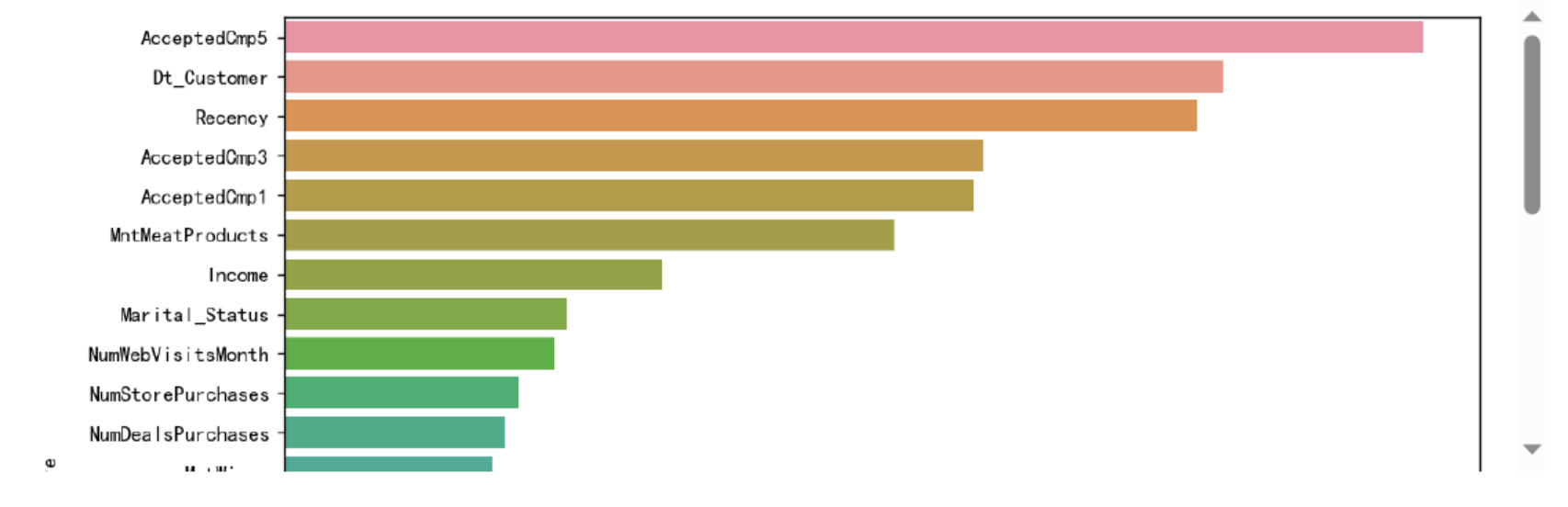
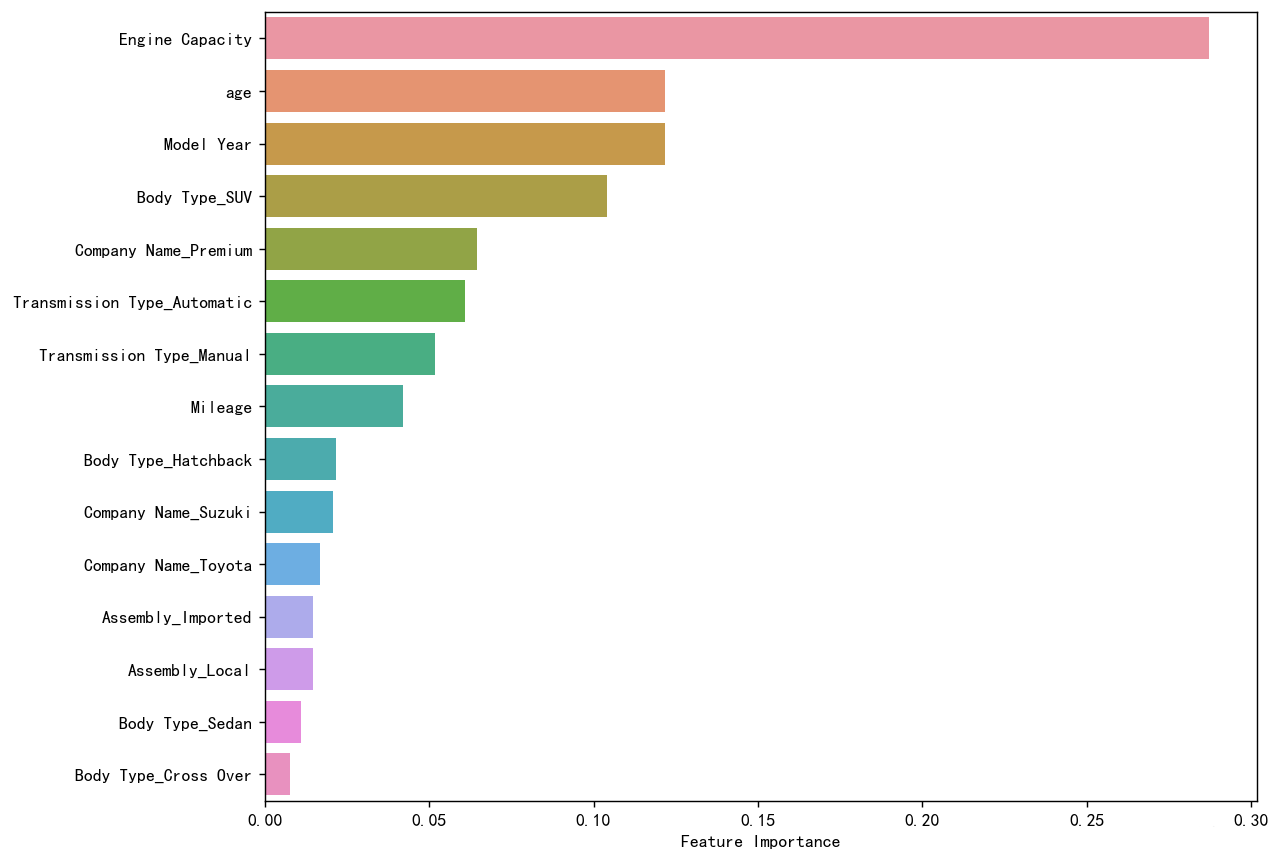
变量重要性分析

sorted_index = model.feature_importances_.argsort()[::-1]
plt.figure(figsize=(10, 8),dpi=128) # 可以调整尺寸以适应所有特征
 
# 使用 seaborn 来绘制条形图
sns.barplot(x=model.feature_importances_[sorted_index], y=X.columns[sorted_index], orient='h')
plt.xlabel('Feature Importance')  # x轴标签
plt.ylabel('Feature')             # y轴标签
plt.show()

pd.DataFrame(model.feature_importances_[sorted_index],index=X.columns[sorted_index],columns=['Feature importance'])

在对模型输出的特征重要性进行分析时，我们可以观察到不同特征对预测结果的多样化影响。首先，Recency 和 Dt_Customer 是最为重要的两个特征，这表明客户最近的活动时间以及与公司的关系长度对模型预测起到了关键作用。这样的结果可能反映了客户忠诚度和近期参与度对预测客户行为的重要性。尤其是，最近的活动可能是客户当前兴趣和购买意向的直接指标，而较长的客户关系则可能指示出稳定的消费行为。

此外，多个与营销活动相关的特征（如 AcceptedCmp5、AcceptedCmp3 和 AcceptedCmp1）的重要性也较高，说明客户对特定营销活动的接受度显著影响了模型的预测。这可能为企业的市场策略提供了有力的支持，提示它们应重视和优化这些营销活动，以提高客户响应率。

在产品消费方面，MntMeatProducts 和 MntWines 的重要性也较为显著，表明某些产品类别的消费金额对客户行为模式有重要影响。这可能意味着特定商品的消费能够反映出客户的消费习惯和偏好，从而为产品推荐和库存管理提供依据。

社会经济因素如 Marital_Status 和 Income 也对模型预测产生了相对重要的影响。婚姻状况和收入水平通常是消费能力与消费决策的核心决定因素，揭示了不同客户群体的消费潜力和模式。

相较之下，其他特征如 Kidhome 和 Education 的重要性较低，表明在该数据集中，它们对客户行为的影响不如前述特征明显。这种特征重要性的差异为企业在资源分配及战略决策方面提供了指导，帮助其识别关键影响因素，优化客户细分和营销活动。综上所述，这些特征的重要性分析不仅能够增强对客户行为的理解，还为进一步的市场和产品策略调整提供了实证支持。

AUC,ROC,KS 评估

2分类问题就逃不开要计算roc曲线，计算auc值和ks。 用如下的代码画出roc曲线跟pr曲线

from sklearn.metrics import roc_curve, auc, precision_recall_curve
y_pred_proba = model.predict_proba(X_test)[:, 1]
# 计算ROC曲线和AUC值
fpr, tpr, _ = roc_curve(y_test, y_pred_proba)
roc_auc = auc(fpr, tpr)
# 计算PR曲线
precision, recall, _ = precision_recall_curve(y_test, y_pred_proba)
 
# 创建1*2的子图
plt.figure(figsize=(10, 4),dpi=128)
 
# 绘制ROC曲线
plt.subplot(1, 2, 1)
plt.plot(fpr, tpr, color='tomato', lw=2, label='AUC = %0.2f' % roc_auc)
plt.plot([0, 1], [0, 1], color='k', lw=1, linestyle='--')
plt.xlim([0.0, 1.0]) ;  plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')  ;  plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic (ROC) Curve')
plt.legend(loc="lower right")
 
# 绘制PR曲线
plt.subplot(1, 2, 2)
plt.plot(recall, precision, color='skyblue', lw=2)
plt.xlim([0.0, 1.0])  ;  plt.ylim([0.0, 1.05])
plt.xlabel('Recall')  ;  plt.ylabel('Precision')
plt.title('Precision-Recall (PR) Curve')
 
# 显示图像
plt.tight_layout()
plt.show()

import scikitplot as skplt
skplt.metrics.plot_ks_statistic(y_test,model.predict_proba(X_test))
plt.show()

AUC=0.87,KS=0.586，模型对于类别的区分能力超级高，可以准确预测客户是否发生购买行为

7.总结

在本次项目中，我们致力于通过构建精准的预测模型来识别潜在的客户购买行为。项目的核心目标是在营销场景下，借助数据驱动的方法提升客户响应率和市场活动的有效性。为了实现这一目标，我们首先在多种模型中进行比较，结合准确率，精准度，召回率和F1值等评价指标，最终选择了梯度提升树（Gradient Boosting）模型，主要因为其在初步评估中展示了最高的准确率，这对我们的应用场景至关重要。

我们进行了数据的清洗整理，分布可视化，一定的特征工程，进行了相关性分析和方差分析，发现学历，婚姻状态对于客户的购买行为没有明显的影响，反而营销活动的次数和活跃度对于客户的购买行为会产生显著性影响。

在模型构建过程中，我们进行了全面的特征工程与选择，重点考察了不同特征对预测客户购买行为的重要性。特征重要性分析显示，客户最近的活动时间（Recency）和与公司的关系长度（Dt_Customer）是最具影响力的因素。这些特征反映了客户的忠诚度和近期参与度，揭示了其购买意图的动态变化。此外，客户对特定营销活动的响应度也是重要的预测变量，强调了有效营销策略在客户行为预测中的关键作用。

通过对模型性能的深入评估，我们计算了AUC（Area Under the ROC Curve）和KS（Kolmogorov-Smirnov）统计量，以验证模型的区分能力。模型取得了令人满意的结果，AUC达到了0.87，而KS值为0.586，均指示出模型在区分有购买行为客户与无购买行为客户方面的优异表现。这些指标不仅验证了模型的预测准确性，也表明其对不同客户群体间差异的敏感度，能够帮助我们精准识别目标客户。

综合来看，模型的高准确率、高AUC值以及显著的KS统计量均表明，我们的梯度提升模型具备强大的预测能力，能够作为有效的工具应用于客户关系管理和市场策略优化。通过对特征重要性的深刻理解，我们不仅能够提升模型的预测精度，还能够为企业在营销活动中的决策提供数据支持，推动更高效的资源分配和策略执行。在后续的工作中，持续的模型优化和特征探索将进一步增强我们的预测能力，为企业带来更大的商业价值。