【Python数据分析案例（2025）】23——客户无监督聚类分析（5种聚类方法）

网盘截屏

案例背景

好久没更新了，出一些常见的案例吧，本次带来的事可视化聚类分析，使用使用 KMeans, DBSCAN, 其他的 clustring 方法去对一个客户的数据进行无监督聚类。

客户聚类分析

客户聚类分析有助于识别客户群体中的不同细分群体，从而实现更精准的营销策略和个性化的客户体验。我们将采用多种聚类分析技术，并通过不同指标进行评估，以确定最优的聚类数量及最佳的聚类方法。

使用如下指标来评估:

Inertia:Inertia衡量聚类之间的紧密程度。惯性值越低，表明聚类之间的紧密程度越高。
Silhouette Score: 轮廓得分用于衡量一个对象与其自身聚类相比与其他聚类的相似程度。该得分范围为-1到1，得分越高表明聚类界限越清晰。
Davies-Bouldin Score: 戴维斯-鲍尔丁得分用于衡量每个聚类与其最相似聚类之间的平均相似度比值。得分越低越好。
Calinski-Harabasz Score: 卡林斯基-哈拉巴什分数（方差比准则）用于衡量群间离散度与群内离散度之和的比值。分数越高表明群的界限越清晰。

数据介绍

大部分数据分析案例就开始写代码，但是不介绍数据是什么就开始写代码都是对人不友好的。

数据长这个样子，就第一列是客户id，其他都是数据的特征。后面会详细介绍。

图片[2]-【Python数据分析案例（2025）】23——客户无监督聚类分析（5种聚类方法）

代码实现

1 – 导入库

需要的话就运行下面，安装一下库

# !pip install --upgrade scikit-learn
# !pip install kneed, plotly

导入包

import numpy as np
import pandas as pd
from scipy.spatial.distance import cdist
import matplotlib.pyplot as plt
import matplotlib.colors as mcolors
import seaborn as sns
import plotly.express as px
from colorama import Fore
 
from sklearn.impute import KNNImputer
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import KMeans, SpectralClustering, AgglomerativeClustering, DBSCAN , HDBSCAN
from sklearn.metrics import silhouette_score, calinski_harabasz_score, davies_bouldin_score
from sklearn.decomposition import PCA
 
#from kneed import KneeLocator
from yellowbrick.cluster import KElbowVisualizer, SilhouetteVisualizer
import warnings

2 – 导入数据

读取数据

# 读取csv数据
df =pd.read_csv('Customer_Data (1).csv')
df

图片[3]-【Python数据分析案例（2025）】23——客户无监督聚类分析（5种聚类方法）

8950行，18列。

3 – 数据描述

图片[4]-【Python数据分析案例（2025）】23——客户无监督聚类分析（5种聚类方法）

数据概况

print('\n 数据概况 : \n')
 
pd.concat([pd.DataFrame(df.count()).T.rename(index={0: 'count'}),
           pd.DataFrame(df.nunique()).T.rename(index={0: 'number of unique'}),
           pd.DataFrame(df.dtypes).T.rename(index={0: 'dtype'}),
           pd.DataFrame(df.isna().sum()).T.rename(index={0: 'null count'}),
           df.describe().drop('count')]).T

图片[5]-【Python数据分析案例（2025）】23——客户无监督聚类分析（5种聚类方法）

可以清晰的看见每个数据的各自的缺失数量，数据类型，中位书，分位数等。

数据概览统计:

所有数据均为数值型，适合进行数值分析和建模。
‘MINIMUM_PAYMENTS’列存在缺失值。
‘BALANCE’、’PURCHASES’、’ONEOFF_PURCHASES’、’INSTALLMENTS_PURCHASES’、’CASH_ADVANCE’、’PAYMENTS’和‘MINIMUM_PAYMENTS’列呈右偏分布，表明少数客户的值远高于其他客户。
‘CREDIT_LIMIT’列大致呈指数分布。
‘BALANCE_FREQUENCY’、’PURCHASES_FREQUENCY’、’ONEOFF_PURCHASES_FREQUENCY’、’PURCHASES_INSTALLMENTS_FREQUENCY’和’CASH_ADVANCE_FREQUENCY’列的值介于0到1之间，可能表示频率或比例。
‘TENURE’列显示大多数客户的账户时长为12个月。

4 -预处理

4.1 – 删除不需要的列

“CUST_ID”列由于在所有行中都是唯一的，因此无法为聚类或分析提供任何有价值的信息。因此该列需要从数据集中删除。

df.drop(columns = ['CUST_ID'], inplace = True)

4.2 – 通过插值填充缺失值

处理数据集中的缺失值，采用了 K-最近邻（KNN）插补方法。KNNImputer 通过考虑最近邻的值来填充缺失值，有效地根据与其他数据点的相似性估计缺失条目。应用 KNN 插补器后，数据集没有缺失值，确保了后续分析的完整性。

Imputer = KNNImputer()
df = pd.DataFrame(Imputer.fit_transform(df), columns=df.columns)
print('插值后的缺失数据量 : ', df.isna().sum().sum())

4.3 – 标准化特征

准备数据进行分析，我们使用了 StandardScaler进行标准化，它通过移除均值和缩放到单位方差来标准化特征。这一步确保每个特征都能平等地贡献于分析，消除了由于特征尺度不同而产生的偏差。

# 标准化
scaler = StandardScaler()
scaled_features = scaler.fit_transform(df)

5 – 可视化

查看不同特征的分布情况，箱线图

# 忽略关于Python或库未来变更的警告，避免输出混乱
warnings.simplefilter(action='ignore', category=FutureWarning)
 
# 设置图表风格为'darkgrid'，提升可读性和美观性
sns.set_style('darkgrid')
 
# 定义自定义颜色调色板，用于可视化
custom_palette = ['#06d6a0', '#118ab2', '#ef476f', '#ffd166', '#073b4c', '#8ecae6', '#fb8500', '#023047']
 
# 获取数据框（df）中需要可视化的列名列表
list_of_columns = list(df.columns)
 
# 创建子图网格：2列，行数等于待可视化列的数量，设置画布大小为(15, 30)
fig, axs = plt.subplots(len(list_of_columns), 2, figsize=(15, 30))
 
# 遍历每个列名及其索引（i）
for i, column_name in enumerate(list_of_columns):
    # 绘制直方图（含KDE密度曲线），使用橙色 (#fb8500)
    sns.histplot(data=df, x=column_name, kde=True, ax=axs[i, 0], color='#fb8500')
    axs[i, 0].set_title(f'Histogram of {column_name}') # 设置直方图标题
    
    # 绘制箱线图，从自定义调色板循环取色
    sns.boxplot(data=df, x=column_name, ax=axs[i, 1], palette=[custom_palette[i % len(custom_palette)]])
    axs[i, 1].set_title(f'Boxplot of {column_name}')  # 设置箱线图标题
 
# 自动调整子图布局，防止元素重叠
plt.tight_layout()
 
# 显示所有图表
plt.show()
 
# 恢复警告过滤器为默认状态（不再忽略FutureWarning）
warnings.simplefilter(action='default', category=FutureWarning)

图片[6]-【Python数据分析案例（2025）】23——客户无监督聚类分析（5种聚类方法）

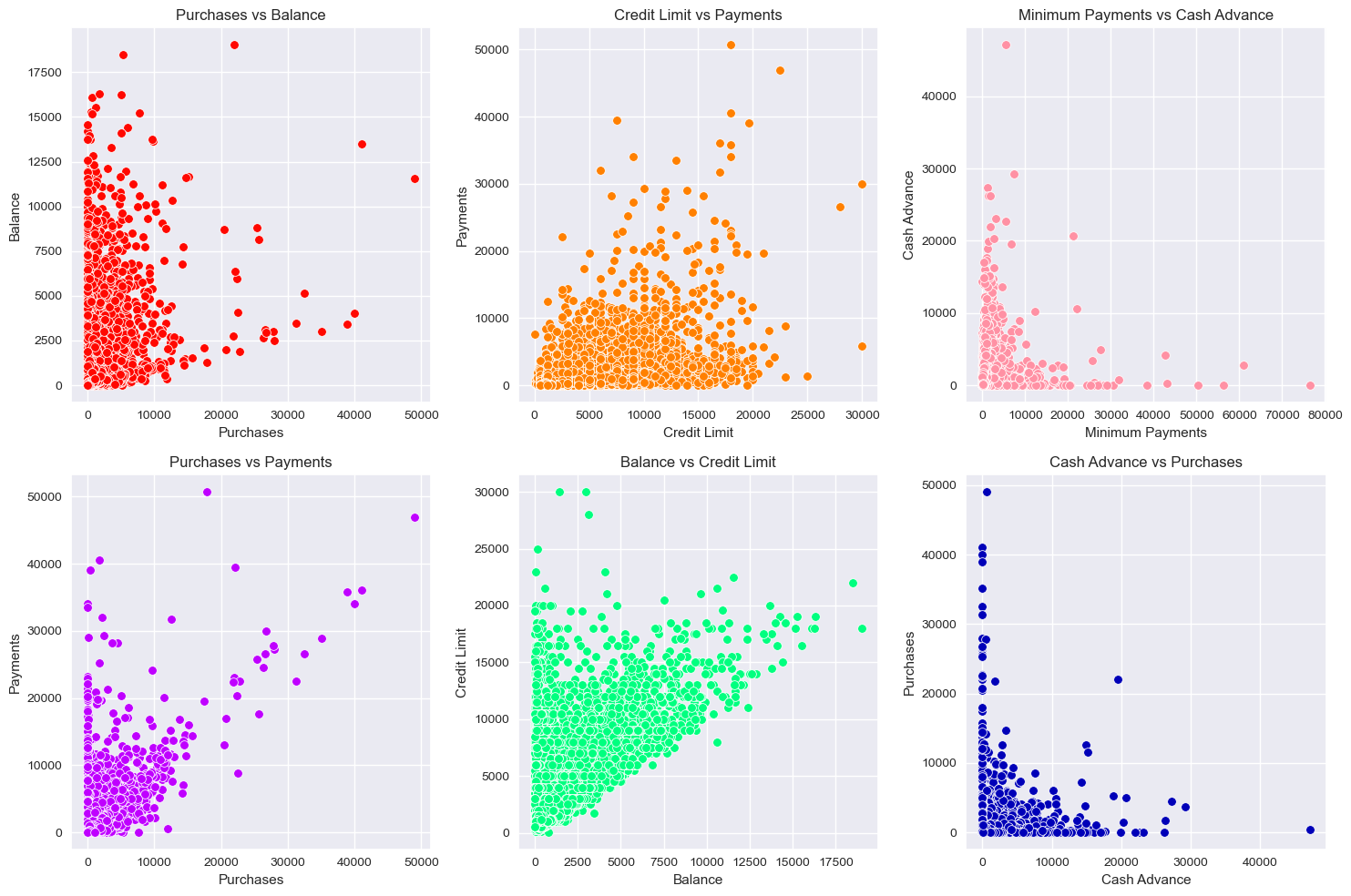
对这些变量22直接画一个散点图，观察相关性。

# # 设置图片风格
# sns.set_style('darkgrid')
 
# 2*3的多子图结构
fig, axs = plt.subplots(2, 3, figsize=(15, 10))
 
# 每个信息列之间的散点图
sns.scatterplot(x='PURCHASES', y='BALANCE', data=df, ax=axs[0, 0], color = '#FF0800')
axs[0, 0].set_title('Purchases vs Balance')
axs[0, 0].set_xlabel('Purchases')
axs[0, 0].set_ylabel('Balance')
 
sns.scatterplot(x='CREDIT_LIMIT', y='PAYMENTS', data=df, ax=axs[0, 1], color = '#FF8000')
axs[0, 1].set_title('Credit Limit vs Payments')
axs[0, 1].set_xlabel('Credit Limit')
axs[0, 1].set_ylabel('Payments')
 
sns.scatterplot(x='MINIMUM_PAYMENTS', y='CASH_ADVANCE', data=df, ax=axs[0, 2], color = '#FF91A4')
axs[0, 2].set_title('Minimum Payments vs Cash Advance')
axs[0, 2].set_xlabel('Minimum Payments')
axs[0, 2].set_ylabel('Cash Advance')
 
sns.scatterplot(x='PURCHASES', y='PAYMENTS', data=df, ax=axs[1, 0], color = '#BF00FF')
axs[1, 0].set_title('Purchases vs Payments')
axs[1, 0].set_xlabel('Purchases')
axs[1, 0].set_ylabel('Payments')
 
sns.scatterplot(x='BALANCE', y='CREDIT_LIMIT', data=df, ax=axs[1, 1], color = '#00FF7F')
axs[1, 1].set_title('Balance vs Credit Limit')
axs[1, 1].set_xlabel('Balance')
axs[1, 1].set_ylabel('Credit Limit')
 
sns.scatterplot(x='CASH_ADVANCE', y='PURCHASES', data=df, ax=axs[1, 2], color = '#0000B8')
axs[1, 2].set_title('Cash Advance vs Purchases')
axs[1, 2].set_xlabel('Cash Advance')
axs[1, 2].set_ylabel('Purchases')
 
# Adjust layout for a clean look
plt.tight_layout()
 
# Display the plots
plt.show()

图片[7]-【Python数据分析案例（2025）】23——客户无监督聚类分析（5种聚类方法）

三维图，观察不同的变量之间的相关和分布情况：

# 定义客户颜色范围
color_scale = 'rainbow'
 
#  为一些最具信息量的列创建一个3D散点图。
fig1 = px.scatter_3d(df, x='PURCHASES', y='BALANCE', z='PAYMENTS', 
                     title='Purchases vs Balance vs Payments',
                     labels={'PURCHASES': 'Purchases', 'BALANCE': 'Balance', 'PAYMENTS': 'Payments'},
                     color='PURCHASES', color_continuous_scale=color_scale,
                     opacity=0.7, size_max=10)
 
fig1.update_layout(scene=dict(
    xaxis_title='Purchases',
    yaxis_title='Balance',
    zaxis_title='Payments',
    xaxis=dict(showgrid=True, gridcolor='lightgrey'),
    yaxis=dict(showgrid=True, gridcolor='lightgrey'),
    zaxis=dict(showgrid=True, gridcolor='lightgrey')
), width=1000, height=800,
    margin=dict(l=50, r=50, b=50, t=50),
    paper_bgcolor='white',
    font=dict(family="Arial, sans-serif", size=12, color="black")
)
fig1.show()
 
fig2 = px.scatter_3d(df, x='CREDIT_LIMIT', y='MINIMUM_PAYMENTS', z='CASH_ADVANCE', 
                     title='Credit Limit vs Minimum Payments vs Cash Advance',
                     labels={'CREDIT_LIMIT': 'Credit Limit', 'MINIMUM_PAYMENTS': 'Minimum Payments', 'CASH_ADVANCE': 'Cash Advance'},
                     color='CREDIT_LIMIT', color_continuous_scale=color_scale,
                     opacity=0.7, size_max=10)
 
fig2.update_layout(scene=dict(
    xaxis_title='Credit Limit',
    yaxis_title='Minimum Payments',
    zaxis_title='Cash Advance',
    xaxis=dict(showgrid=True, gridcolor='lightgrey'),
    yaxis=dict(showgrid=True, gridcolor='lightgrey'),
    zaxis=dict(showgrid=True, gridcolor='lightgrey')
), width=1000, height=800,
    margin=dict(l=50, r=50, b=50, t=50),
    paper_bgcolor='white',
    font=dict(family="Arial, sans-serif", size=12, color="black")
)
fig2.show()
 
fig3 = px.scatter_3d(df, x='PURCHASES', y='PAYMENTS', z='BALANCE', 
                     title='Purchases vs Payments vs Balance',
                     labels={'PURCHASES': 'Purchases', 'PAYMENTS': 'Payments', 'BALANCE': 'Balance'},
                     color='PAYMENTS', color_continuous_scale=color_scale,
                     opacity=0.7, size_max=10)
 
fig3.update_layout(scene=dict(
    xaxis_title='Purchases',
    yaxis_title='Payments',
    zaxis_title='Balance',
    xaxis=dict(showgrid=True, gridcolor='lightgrey'),
    yaxis=dict(showgrid=True, gridcolor='lightgrey'),
    zaxis=dict(showgrid=True, gridcolor='lightgrey')
), width=1000, height=800,
    margin=dict(l=50, r=50, b=50, t=50),
    paper_bgcolor='white',
    font=dict(family="Arial, sans-serif", size=12, color="black")
)
fig3.show()

图片[8]-【Python数据分析案例（2025）】23——客户无监督聚类分析（5种聚类方法）

这个图是动态可以拖动的，可以观察3个变量之间的相互关系。

下面开始使用不同的算法进行聚类。

6 – KMeans

下面是全流程，聚类完成后，查看结果，计算评价指标，可视化，全在这个代码里面了

results = []
 
# 可视化参数
init_methods = ['random', 'k-means++']
 
# 遍历不同的初始化方法和聚类数量以评估指标
for init in init_methods:
    for k in range(2, 11):
        kmeans = KMeans(n_clusters=k, init=init, n_init=10, max_iter=500, random_state=42)
        kmeans_labels = kmeans.fit_predict(scaled_features)
        silhouette = silhouette_score(scaled_features, kmeans_labels)
        db_score = davies_bouldin_score(scaled_features, kmeans_labels)
        ch_score = calinski_harabasz_score(scaled_features, kmeans_labels)
        results.append((init, k, kmeans.inertia_, silhouette, db_score, ch_score))
 
# 结果表
results_df = pd.DataFrame(results, columns=['Init Method', 'Number of Clusters', 'Inertia', 'Silhouette Score', 'Davies Bouldin Score', 'Calinski Harabasz Score'])
 
# 展示结果
print(Fore.RED + """
***********************************************************************************************************
                                      聚类评价指标：
***********************************************************************************************************
""")
display(results_df.sort_values(by = ['Silhouette Score'], ascending = False))
 
## 根据轮廓评分确定最佳参数
best_result = results_df.loc[results_df['Silhouette Score'].idxmax()]
best_init = best_result['Init Method']
best_k = best_result['Number of Clusters']
print(f'\nBest Init Method: {best_init}')
print(f'最佳聚类数量 (based on Silhouette Score): {best_k}\n')
 
# 使用Yellowbrick可视化肘部方法
print(Fore.RED + """
***********************************************************************************************************
                                       手肘图方法可视化：
***********************************************************************************************************
""")
elbow_visualizer = KElbowVisualizer(KMeans(init=best_init, n_init=10, max_iter=500, random_state=42), k=(2, 11), timings=False)
elbow_visualizer.fit(scaled_features)
elbow_visualizer.finalize()
 
plt.show()
 
# 画出可视化评价指标
 
fig, axs = plt.subplots(2, 2, figsize=(14, 10))
    
sns.lineplot(x='Number of Clusters', y='Inertia', hue='Init Method', data=results_df, ax=axs[0, 0], marker='o')
axs[0, 0].set_title('Elbow Method (Inertia)')
axs[0, 0].set_xlabel('Number of Clusters')
axs[0, 0].set_ylabel('Inertia')
    
sns.lineplot(x='Number of Clusters', y='Silhouette Score', hue='Init Method', data=results_df, ax=axs[0, 1], marker='o')
axs[0, 1].set_title('Silhouette Score')
axs[0, 1].set_xlabel('Number of Clusters')
axs[0, 1].set_ylabel('Silhouette Score')
    
sns.lineplot(x='Number of Clusters', y='Davies Bouldin Score', hue='Init Method', data=results_df, ax=axs[1, 0], marker='o')
axs[1, 0].set_title('Davies Bouldin Score')
axs[1, 0].set_xlabel('Number of Clusters')
axs[1, 0].set_ylabel('Davies Bouldin Score')
    
sns.lineplot(x='Number of Clusters', y='Calinski Harabasz Score', hue='Init Method', data=results_df, ax=axs[1, 1], marker='o')
axs[1, 1].set_title('Calinski Harabasz Score')
axs[1, 1].set_xlabel('Number of Clusters')
axs[1, 1].set_ylabel('Calinski Harabasz Score')
    
plt.tight_layout()
plt.show()
 
# 画评估指标
 
# 总结结果
print(Fore.RED + """
***********************************************************************************************************
                                       结果解释：
***********************************************************************************************************
""")
print(Fore.BLUE + """1. 随着聚类数量的增加，惯性（Inertia）逐渐减小，这是预期结果。
因为聚类数量越多，每个簇的规模越小且内部更紧凑。""" + '\n')
print("""2. 轮廓系数（Silhouette Score）在聚类数从2增加到3时有所提升，之后波动变化。
最高得分0.250481出现在3个聚类时，这可能是较优选择，尽管其他聚类数的得分也比较接近。""")
print('\n' + """3. 戴维森堡丁指数（Davies-Bouldin Score）先下降后波动。
最低值1.349645（数值越低表示聚类效果越好）出现在10个聚类时。""" + '\n')
print("""4. 卡林斯基-哈拉巴斯指数（Calinski-Harabasz Score）在2个聚类时最高，并随聚类数增加而下降。
这可能表明2个聚类能较好地区分数据。""" + '\n')
print(f"根据分析结果，我们选择{best_k}个聚类，初始化方法为'{best_init}'。" + '\n')
print(Fore.RESET)
 
# 使用选定的聚类数和初始化方法执行K均值聚类
kmeans = KMeans(n_clusters=best_k, init=best_init, n_init=10, max_iter=500, random_state=42)
kmeans_labels = kmeans.fit_predict(scaled_features)
    
# 画 PCA
pca = PCA(n_components=2)
pca_transformed = pca.fit_transform(scaled_features)
    
df_pca = pd.DataFrame(pca_transformed, columns=['PCA1', 'PCA2'])
df_pca['Cluster'] = kmeans_labels
 
centroids = kmeans.cluster_centers_
centroids_pca = pca.transform(centroids)
    
plt.figure(figsize=(8, 6))
sns.scatterplot(x='PCA1', y='PCA2', hue='Cluster', palette='tab10', data=df_pca)
plt.scatter(centroids_pca[:, 0], centroids_pca[:, 1], s=300, c= '#CC33CC', marker='X', label='Centroids')
plt.title(f'KMeans Clustering with {best_k} Clusters and {best_init} Init (PCA-reduced Data)')
plt.show()

图片[9]-【Python数据分析案例（2025）】23——客户无监督聚类分析（5种聚类方法）

图片[10]-【Python数据分析案例（2025）】23——客户无监督聚类分析（5种聚类方法）

结果的解释也写在代码里面了，上面图片是评价指标和聚类结果可视化已经解释。

7 – SpectralClustering

Spectral Clustering（谱聚类）是一种基于图论的聚类方法，通过利用数据的相似性矩阵（affinity matrix）和图拉普拉斯矩阵（Graph Laplacian）的特征结构，将数据映射到低维空间后进行聚类（如K-means）。其核心思想是将数据视为图中的节点，通过图的谱（特征值分解）来划分结构。

也是一样，变量聚类2-11，看看哪个效果最好，计算评价指标，可视化结果和解释。

results = []
 
#  遍历不同的初始化方法和聚类数量以评估指标
for k in range(2, 11):
    spectral = SpectralClustering(n_clusters=k, affinity='nearest_neighbors', random_state=42, n_init=10)
    spectral_labels = spectral.fit_predict(scaled_features)
    
    silhouette = silhouette_score(scaled_features, spectral_labels)
    db_score = davies_bouldin_score(scaled_features, spectral_labels)
    ch_score = calinski_harabasz_score(scaled_features, spectral_labels)
    
    results.append((k, silhouette, db_score, ch_score))
 
# 结果表
results_df = pd.DataFrame(results, columns=['Number of Clusters', 'Silhouette Score', 'Davies Bouldin Score', 'Calinski Harabasz Score'])
 
# 展示结果
print(Fore.RED + """
***********************************************************************************************************
                                    聚类评价指标：
***********************************************************************************************************
""")
display(results_df.sort_values(by = ['Silhouette Score'], ascending = False))
 
## 根据轮廓评分确定最佳参数
best_k = results_df.loc[results_df['Silhouette Score'].idxmax(), 'Number of Clusters']
print(f'\n最佳聚类数量 (based on Silhouette Score): {best_k}\n')
 
# 使用Yellowbrick可视化肘部方法
def plot_evaluation_metrics(results_df):
    fig, axs = plt.subplots(1, 3, figsize=(18, 5))
    
    sns.lineplot(x='Number of Clusters', y='Silhouette Score', data=results_df, ax=axs[0], marker='o')
    axs[0].set_title('Silhouette Score')
    axs[0].set_xlabel('Number of Clusters')
    axs[0].set_ylabel('Silhouette Score')
    
    sns.lineplot(x='Number of Clusters', y='Davies Bouldin Score', data=results_df, ax=axs[1], marker='o')
    axs[1].set_title('Davies Bouldin Score')
    axs[1].set_xlabel('Number of Clusters')
    axs[1].set_ylabel('Davies Bouldin Score')
    
    sns.lineplot(x='Number of Clusters', y='Calinski Harabasz Score', data=results_df, ax=axs[2], marker='o')
    axs[2].set_title('Calinski Harabasz Score')
    axs[2].set_xlabel('Number of Clusters')
    axs[2].set_ylabel('Calinski Harabasz Score')
    
    plt.tight_layout()
    plt.show()
 
# 画出可视化评价指标
plot_evaluation_metrics(results_df)
 
# 总结结果
print(Fore.RED + """
***********************************************************************************************************
                                   结果解释：
***********************************************************************************************************
""")
print(Fore.BLUE + """1. 轮廓系数(Silhouette Score)用于评估每个数据点与其所属簇的相似度相比其他簇的程度。
数值越高(最大为1)表示聚类效果越好，簇间区分越明显。""" + '\n') 
print("""2. 戴维森堡丁指数(Davies-Bouldin Score)通过计算各簇与其最相似簇的平均相似度来评估聚类效果。
数值越低(最小为0)表示聚类质量越好。""" + '\n')
print("""3. 卡林斯基-哈拉巴斯指数(Calinski-Harabasz Score)通过计算簇间离散度与簇内离散度的比值来评估聚类效果。
数值越高表示聚类效果越好。""" + '\n')
print(f"综合评估结果，我们最终选择{best_k}个聚类方案。" + '\n')
print(Fore.RESET)
 
# # 使用选定的聚类数和初始化方法执行Spectral聚类
spectral = SpectralClustering(n_clusters=best_k, affinity='nearest_neighbors', random_state=42, n_init=10)
spectral_labels = spectral.fit_predict(scaled_features)
    
# 画 PCA
pca = PCA(n_components=2)
pca_transformed = pca.fit_transform(scaled_features)
    
df_pca = pd.DataFrame(pca_transformed, columns=['PCA1', 'PCA2'])
df_pca['Cluster'] = spectral_labels
    
plt.figure(figsize=(8, 6))
sns.scatterplot(x='PCA1', y='PCA2', hue='Cluster', palette='tab10', data=df_pca)
plt.title(f'Spectral Clustering with {best_k} Clusters (PCA-reduced Data)')
plt.show()

图片[11]-【Python数据分析案例（2025）】23——客户无监督聚类分析（5种聚类方法）

图片[12]-【Python数据分析案例（2025）】23——客户无监督聚类分析（5种聚类方法）

8 – AgglomerativeClustering

Agglomerative Clustering（层次凝聚聚类） 是一种自底向上的层次聚类方法，通过逐步合并最相似的簇来构建树状图（Dendrogram），最终形成聚类结构。与谱聚类不同，它直接基于数据点之间的距离或相似性进行迭代合并，无需降维或矩阵分解。

和上面的流程一样，尝试聚类2-11类，看看哪个效果最好，计算评价指标，可视化结果和解释。

results = []
 
# 遍历不同的初始化方法和聚类数量以评估指标
for k in range(2, 11):
    agglomerative_clustering = AgglomerativeClustering(n_clusters=k)
    agglomerative_labels = agglomerative_clustering.fit_predict(scaled_features)
    
    silhouette = silhouette_score(scaled_features, agglomerative_labels)
    db_score = davies_bouldin_score(scaled_features, agglomerative_labels)
    ch_score = calinski_harabasz_score(scaled_features, agglomerative_labels)
    
    results.append((k, silhouette, db_score, ch_score))
 
# 结果表
results_df = pd.DataFrame(results, columns=['Number of Clusters', 'Silhouette Score', 'Davies Bouldin Score', 'Calinski Harabasz Score'])
 
# 展示结果
print(Fore.RED + """
***********************************************************************************************************
                             AgglomerativeClustering 聚类的评价指标
***********************************************************************************************************
""")
display(results_df.sort_values(by = ['Silhouette Score'], ascending = False))
 
## 根据轮廓评分确定最佳参数
best_num_clusters = results_df.loc[results_df['Silhouette Score'].idxmax(), 'Number of Clusters']
print(f'\n 最佳聚类数量 (based on Silhouette Score): {best_num_clusters}\n')
 
fig, axs = plt.subplots(1, 3, figsize=(18, 5))
    
sns.lineplot(x='Number of Clusters', y='Silhouette Score', data=results_df, ax=axs[0], marker='o')
axs[0].set_title('Silhouette Score')
axs[0].set_xlabel('Number of Clusters')
axs[0].set_ylabel('Silhouette Score')
    
sns.lineplot(x='Number of Clusters', y='Davies Bouldin Score', data=results_df, ax=axs[1], marker='o')
axs[1].set_title('Davies Bouldin Score')
axs[1].set_xlabel('Number of Clusters')
axs[1].set_ylabel('Davies Bouldin Score')
    
sns.lineplot(x='Number of Clusters', y='Calinski Harabasz Score', data=results_df, ax=axs[2], marker='o')
axs[2].set_title('Calinski Harabasz Score')
axs[2].set_xlabel('Number of Clusters')
axs[2].set_ylabel('Calinski Harabasz Score')
    
plt.tight_layout()
plt.show()
 
# 最优聚类数量  Perform AgglomerativeClustering
agglomerative_clustering = AgglomerativeClustering(n_clusters=best_num_clusters)
agglomerative_labels = agglomerative_clustering.fit_predict(scaled_features)
 
# PCA可视化 对于 AgglomerativeClustering的结果
pca = PCA(n_components=2)
pca_transformed = pca.fit_transform(scaled_features)
 
df_pca = pd.DataFrame(pca_transformed, columns=['PCA1', 'PCA2'])
df_pca['Cluster'] = agglomerative_labels
 
plt.figure(figsize=(8, 6))
sns.scatterplot(x='PCA1', y='PCA2', hue='Cluster', palette='tab10', data=df_pca)
plt.title(f'AgglomerativeClustering with {best_num_clusters} Clusters (PCA-reduced Data)')
plt.show()
 
# 总结结果
print(Fore.RED + """
***********************************************************************************************************
                                  结果解释：
***********************************************************************************************************
""")
print(Fore.BLUE + f"""1. 最优聚类数量: {best_num_clusters}""" + '\n')
print(f"""2. 轮廓系数(Silhouette Score): {results_df.loc[results_df['Number of Clusters'] == best_num_clusters, 'Silhouette Score'].values[0]:.6f} - 该值越接近1表示聚类效果越好""" + '\n')
print(f"""3. 戴维森堡丁指数(Davies-Bouldin Score): {results_df.loc[results_df['Number of Clusters'] == best_num_clusters, 'Davies Bouldin Score'].values[0]:.6f} - 该值越小表示聚类质量越高""" + '\n')
print(f"""4. 卡林斯基-哈拉巴斯指数(Calinski-Harabasz Score): {results_df.loc[results_df['Number of Clusters'] == best_num_clusters, 'Calinski Harabasz Score'].values[0]:.6f} - 该值越大表示聚类效果越好""" + '\n')
print(Fore.RESET)

9 – DBSCAN

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）是一种基于密度的聚类算法，能够识别任意形状的簇，并自动剔除噪声点（离群点）。与K-means和层次聚类不同，它不假设簇是凸形的，也不需要预先指定簇的数量，而是通过数据分布的紧密程度来划分簇。

一样的流程。

results = []
best_silhouette = -1
best_eps = None
best_min_samples = None
best_dbscan_labels = None
 
# 遍历不同的初始化方法和聚类数量以评估指标
for eps in np.arange(0.1, 2.0, 0.1):
    for min_samples in range(5, 501, 50):
        dbscan = DBSCAN(eps=eps, min_samples=min_samples)
        dbscan_labels = dbscan.fit_predict(scaled_features)
        
        # Filter out noise points (label == -1)
        filtered_features = scaled_features[dbscan_labels != -1]
        filtered_labels = dbscan_labels[dbscan_labels != -1]
        
        # Evaluate metrics only if there are clusters found
        if len(np.unique(filtered_labels)) > 1:
            silhouette = silhouette_score(filtered_features, filtered_labels)
            db_score = davies_bouldin_score(filtered_features, filtered_labels)
            ch_score = calinski_harabasz_score(filtered_features, filtered_labels)
            
            results.append((eps, min_samples, silhouette, db_score, ch_score, len(np.unique(filtered_labels))))
            
            # Update the best parameters based on silhouette score
            if silhouette > best_silhouette:
                best_silhouette = silhouette
                best_eps = eps
                best_min_samples = min_samples
                best_dbscan_labels = dbscan_labels
 
# 结果表
results_df = pd.DataFrame(results, columns=['eps', 'min_samples', 'Silhouette Score', 'Davies Bouldin Score', 'Calinski Harabasz Score', 'Number of Clusters'])
 
# 展示结果
print(Fore.RED + """
***********************************************************************************************************
                                    聚类评价指标
***********************************************************************************************************
""")
display(results_df.sort_values(by=['Silhouette Score'], ascending=False))
 
print(f"Best eps value: {best_eps}")
print(f"Best min_samples value: {best_min_samples}")
print(f"Best Silhouette Score: {best_silhouette}")
 
# PCA 可视化 对于  DBSCAN 最优结果
pca = PCA(n_components=2)
pca_transformed = pca.fit_transform(scaled_features)
 
df_pca = pd.DataFrame(pca_transformed, columns=['PCA1', 'PCA2'])
df_pca['Cluster'] = best_dbscan_labels
 
plt.figure(figsize=(8, 6))
sns.scatterplot(x='PCA1', y='PCA2', hue='Cluster', palette='tab10', data=df_pca)
plt.title(f'DBSCAN Clustering with eps={best_eps}, min_samples={best_min_samples} (PCA-reduced Data)')
plt.show()
 
# 总结结果
print(Fore.RED + """
***********************************************************************************************************
                                  结果解释：
***********************************************************************************************************
""")
print(Fore.BLUE + f"""1. DBSCAN算法确定的最优邻域半径(eps): {best_eps}""" + '\n')
print(f"""2. DBSCAN算法确定的最优最小样本数(min_samples): {best_min_samples}""" + '\n')
print(f"""3. DBSCAN聚类数量(不含噪声点): {results_df[(results_df['eps'] == best_eps) & (results_df['min_samples'] == best_min_samples)]['Number of Clusters'].values[0]}""" + '\n')
print(f"""4. 轮廓系数(Silhouette Score): {best_silhouette:.6f} - 数值越接近1表示聚类效果越好""" + '\n')
print(f"""5. 戴维森堡丁指数(Davies-Bouldin Score): {results_df[(results_df['eps'] == best_eps) & (results_df['min_samples'] == best_min_samples)]['Davies Bouldin Score'].values[0]:.6f} - 数值越小表示聚类质量越高""" + '\n')
print(f"""6. 卡林斯基-哈拉巴斯指数(Calinski-Harabasz Score): {results_df[(results_df['eps'] == best_eps) & (results_df['min_samples'] == best_min_samples)]['Calinski Harabasz Score'].values[0]:.6f} - 数值越大表示聚类效果越好""" + '\n')
print(Fore.RESET)

图片[13]-【Python数据分析案例（2025）】23——客户无监督聚类分析（5种聚类方法）

当应用于该数据集时，DBSCAN生成了大量-1聚类，表明大量数据点被识别为噪声。这表明DBSCAN可能不适合该数据集，因为它无法形成清晰定义的聚类，并将其中的许多点标记为异常值。

这个算法感觉很多数据集都是这样，大多数情况下不太好用。

10 – HDBSCAN

HDBSCAN（Hierarchical Density-Based Spatial Clustering of Applications with Noise）是 DBSCAN 的升级版本，结合了层次聚类和密度聚类的优点。它改进了传统 DBSCAN 对参数 eps 的敏感性，能够自动确定最佳聚类，并识别不同密度的簇，同时保留噪声点的识别能力。

results = []
 
# 遍历不同的初始化方法和聚类数量以评估指标
for min_cluster_size in range(2, 11):
    for min_samples in range(2, 11):
        hdbscan_clustering = HDBSCAN(min_cluster_size=min_cluster_size, min_samples=min_samples)
        hdbscan_labels = hdbscan_clustering.fit_predict(scaled_features)
        
        # 指标计算过滤掉噪音点
        valid_points = hdbscan_labels != -1
        
        if valid_points.sum() > 0:
            silhouette = silhouette_score(scaled_features[valid_points], hdbscan_labels[valid_points])
            db_score = davies_bouldin_score(scaled_features[valid_points], hdbscan_labels[valid_points])
            ch_score = calinski_harabasz_score(scaled_features[valid_points], hdbscan_labels[valid_points])
        else:
            silhouette = -1
            db_score = -1
            ch_score = -1
        
        results.append((min_cluster_size, min_samples, silhouette, db_score, ch_score, len(np.unique(hdbscan_labels[valid_points]))))
 
# 结果表
results_df = pd.DataFrame(results, columns=['Min Cluster Size', 'Min Samples', 'Silhouette Score', 'Davies Bouldin Score', 'Calinski Harabasz Score', 'Number of Clusters'])
 
# 展示结果
print(Fore.RED + """
***********************************************************************************************************
                                        聚类评价指标：
***********************************************************************************************************
""")
display(results_df.sort_values(by=['Silhouette Score'], ascending=False))
 
# 基于 silhouette 分数的最优参数
best_params = results_df.loc[results_df['Silhouette Score'].idxmax()]
best_min_cluster_size = best_params['Min Cluster Size']
best_min_samples = best_params['Min Samples']
print(f'\nBest Min Cluster Size (based on Silhouette Score): {best_min_cluster_size}')
print(f'Best Min Samples (based on Silhouette Score): {best_min_samples}\n')
 
#  HDBSCAN 聚类的最优参数 w
hdbscan_clustering = HDBSCAN(min_cluster_size=int(best_min_cluster_size), min_samples=int(best_min_samples))
hdbscan_labels = hdbscan_clustering.fit_predict(scaled_features)
 
# 对于 HDBSCAN 的结果 的  PCA 可视化
pca = PCA(n_components=2)
pca_transformed = pca.fit_transform(scaled_features)
 
df_pca = pd.DataFrame(pca_transformed, columns=['PCA1', 'PCA2'])
df_pca['Cluster'] = hdbscan_labels
 
plt.figure(figsize=(8, 6))
sns.scatterplot(x='PCA1', y='PCA2', hue='Cluster', palette='tab10', data=df_pca)
plt.title(f'HDBSCAN with Min Cluster Size {best_min_cluster_size} and Min Samples {best_min_samples} (PCA-reduced Data)')
plt.show()
 
# 总结结果
print(Fore.RED + """
***********************************************************************************************************
                                    结果解释：
***********************************************************************************************************
""")
print(Fore.BLUE + f"""1. 最优最小簇大小(Min Cluster Size): {best_min_cluster_size}""" + '\n')
print(f"""2. 最优最小样本数(Min Samples): {best_min_samples}""" + '\n')
print(f"""3. 轮廓系数(Silhouette Score): {best_params['Silhouette Score']:.6f} - 数值越接近1表示簇结构越清晰""" + '\n')
print(f"""4. 戴维森堡丁指数(Davies-Bouldin Score): {best_params['Davies Bouldin Score']:.6f} - 数值越小表示聚类质量越好""" + '\n')
print(f"""5. 卡林斯基-哈拉巴斯指数(Calinski-Harabasz Score): {best_params['Calinski Harabasz Score']:.6f} - 数值越大表示聚类效果越优""" + '\n')
print(Fore.RESET)